1. Introducción
El impacto de lo que se ha resumido en denominar “pensamiento complejo” ha permitido no solamente comprender la naturaleza del mundo circundante desde una óptica diferente, sino también la posibilidad de desarrollar herramientas para evaluar procesos para los cuales el paradigma clásico de modelación newtoniana resultaba insuficiente. Este es un resumen nuestra experiencia en la aplicación del método de identificación no lineal para el estudio de señales fisiológicas complejas.
El organismo humano genera diferentes tipos de señales, algunas de las cuales se modifican ante la presencia de enfermedad u otras condiciones como el ejercicio físico, o el sueño . Entre las señales más interesantes se encuentran aquellas que se obtienen a partir de los sistemas respiratorio y cardiovascular, como el electrocardiograma, la señal fotopletismográfica, los flujos respiratorios.
La medicina del siglo XIX aún era un arte, bello y humanista, pero empírico y desligado en ocasiones del pensamiento “racional” que se había entronizado desde el siglo XVII en la mecánica y en el resto de las ciencias naturales.
El siglo XX marcó el inicio de la incorporación de la metodología científica a la práctica médica, asi, por ejemplo, en 1924 se le otorgó al biofísico holandés Willem Einthoven el Premio Nobel en medicina por haber construido el primer electrocardiograma práctico y haber desarrollado los fundamentos de la interpretación clínica de la señal electro-cardiográfica. En 1929 Hans Berger publica la famosa serie de artículos “Das Elektroencefalogram des Menshen” donde resume más de cinco años de minucioso registro de la actividad eléctrica cerebral.
Sin embargo, la manera en que las bioseñales se interpretan en medicina ha sido bien diferente de la manera en que los físicos las han visto. En medicina se habla de “ondas Q, R, S” y se comenta sobre la inversión de la onda T en el electrocardiograma, o sobre distintos patrones respiratorios. De hecho, el método desarrollado por Einthoven entró a la cardiología no como un sistema de elaboraciones matemáticas derivadas de las ecuaciones de Maxwell, sino como un procedimiento gráfico al que se le denominó “El Triángulo de Einthoven” (Cualquier alusión al Triángulo de Las Bermudas es mera coincidencia).
Es posible que para los físicos de mediados del siglo XX esa manera tan poética de interpretar los fenómenos que proceden según las estrictas ecuaciones de Maxwell les pareciera una evidencia de la profunda ignorancia de los médicos en el campo de las ciencias “duras”.
Hacia mediados del siglo XX, gracias al monumental trabajo de Hodgkin y Huxley, se logró dilucidar la naturaleza biofísica del potencial de acción, y este estudio condujo, por una parte, a la investigación detallada de las bases sub-celulares, moleculares y sub-moleculares de la excitabilidad, mientras que por otra, se desarrollaron estudios de modelación desde abajo hacia arriba, donde se pretendía explicar la emergencia de funciones complejas, partiendo del modelo de Hodgkin y Huxley y siguiendo un riguroso paradigma newtoniano.
Hoy, a la luz del pensamiento complejo, la explicación para del menor éxito del paradigma newtoniano en las ciencias médicas puede ser distinta, pues conocemos que ese enfoque tradicional resulta insuficiente para describir algunos fenómenos del mundo cotidiano. Los médicos, que eran los menos preparados en el campo de la física y la matemática, resolvieron esa dificultad asumiendo enfoques ad hoc que permitían caracterizar los fenómenos observados a partir de conceptos fácilmente visualizables aún cuando no siempre fueran muy rigurosos para la sacrosanta pero en ocasiones no tan útil ciencia pura.
En el análisis de las señales biomédicas se han establecido conceptos que no existían en la física clásica, como son “grafo-elemento”, “ritmo”, “complejo”, etc. Esos conceptos por muchos años carecieron de una contraparte físico-matemática, pero sí contaban con una indudable utilidad para el diagnóstico y pronóstico de diferentes enfermedades.
Entre algunos especialistas, por otra parte, existían serias dudas acerca de la utilidad del electroencefalograma. En la década de 1970 alguien llegó a sugerir que un electroencefalograma completamente “normal” puede obtenerse si se colocan electrodos a una pelota de futbol rellena con solución salina. Otros fisiólogos expresaban sus sospechas al afirmar que evaluar el sistema nervioso a partir de un EEG era algo así como juzgar el proceso productivo en una fábrica de embutidos a partir del análisis del humo de su chimenea. El símil parecía lo suficientemente convincente como para distraer al más entusiasta recién graduado de todo intento a dedicarse al análisis biofísico de las señales fisiológicas.
En 1984 el matemático holandés Floris Takens formuló un teorema que, aparentemente, constituyó uno de los grandes jalones en la historia de la ciencia moderna. Takens demostró que para un sistema dinámico donde un numero n de variables están relacionadas de modo no lineal, es posible obtener una caracterización bastante completa de ese sistema aun cuando sea imposible observar todas las variables implicadas. Más aún, si se cuenta con una versión discretizada de una sola de esas variables (de hecho cualquiera), es posible obtener una versión topológicamente equivalente del retrato de fase, así como evaluar exactamente dos invariantes dinámicas del sistema, a saber su dimensión de correlación y el espectro de los exponentes de Lyapunov.
Para muchos investigadores involucrados en el estudio de procesos fisiológicos, esa fue la evidencia de que es posible a partir del análisis de las series temporales de una señal emitida por un órgano, obtener información más allá de la simple variable que esa señal mide. En el símil de la fábrica de embutidos, es posible que no se logre por esta vía detectar quién es el operario que ha cometido un error de manipulación, pero sí existe la posibilidad de percatarse que algún engranaje ha dejado de funcionar adecuadamente en el proceso de fabricación de salamis.
Esta posibilidad atrajo a muchedumbres de entusiastas que muy pronto encontraron evidencias de caos por todas partes, y el caos se puso de moda. A ese fervor inicial le siguió una serie de trabajos demostrando la limitación de los enfoques anteriores, y sugiriendo nuevos métodos, en esta ocasión sesgados hacia la dirección opuesta, por lo que casi ninguna de las evidencias anteriores de caos quedaron en pie.
La frase lapidaria de Vesin y Vives pudiera resumir ese espíritu “Heart rate variability is anything except chaos”. Eso condujo a que el caos se interpretara como algo que ha quedado fuera de moda, y el interés por el tema amainara. Al mismo tiempo, con tanta pasión y tanto esfuerzo creativo desplegado tanto por partidarios como por escépticos, a la altura de 2021 se cuenta con un arsenal de herramientas, se han acumulado datos y existe la posibilidad de buscar respuestas a preguntas concretas, las cuales pueden ser tanto interesantes desde el punto de vista teórico como esperanzadoras para mejorar la calidad de vida de millones de pacientes.
Esta es una breve revisión de algunas de nuestras experiencias en la aplicación de la metodología de identificación no lineal al estudio de señales electrofisiológicas desarrolladas por nuestra Comunidad de Software Libre.
2. Naturaleza de la señal fotopletismográfica
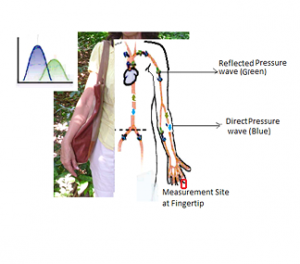
La señal fotopletismográfica (Photoplethysmographic Signal, PPG) registra los cambios pulsatiles en el volume de los capilares y arteriolas que irrigan un area dada, generalmente un dedo. La señal PPG está determinada en gran medida por la presión arterial. A diferencia de otras señales cardiovasculares, el registro de la señal PPG es relativamente simple, y, si se aplican métodos de análisis adecuados, de ella puede extraerse una información similar a la que aportan métodos mucho más costosos. De hecho, a partir de esta señal es posible estimar la frecuencia cardiaca, y se plantea que es posible también medir la presión arterial. El éxito depende de la conducción de un análisis adecuado.
Representación esquemática de la señal PPG
Figura 1. Representación esquemática de la señal PPG
La red arterial aparentemente cumple con ciertos principios de optimalidad como son el mínimo esfuerzo de la bomba cardiaca, la mínima área de irrigación, etc. Este comportamiento óptimo no necesariamente emerge de un diseño inteligente, o de un programa genético sofisticado. De hecho, puede deberse a reglas muy simples de la mecánica que operan a nivel local y que abren el camino a una auto-organización global, una caracte’isica inherente a muchos sistemas complejos del mundo real.
La estructura de las redes arteriales ha sido estudiada desde diferentes puntos de vista, y algunas señales cardiovasculares han sido esxaminadas en el contexto The structure of arterial networks has been studied from different viewpointsde la anatom’ia de diferentes arterias y venas. Así, por ejemplo, la presencia de inflexiones en las señales de ondas de presión tiene una relación aparente con la aparición de ondas reflejadas que se originan en las bifurcaciones de la aorta. Algunos ‘indices conocidos, como el llamadi índice de aumento (Augmentation Index) estudian la supuesta onda reflejada, y cambios en este índice asociados al envejecimiento fisiológico pudieran ser consecuencia de las propiedades anatómicas y visco-elásticos de las arterias.
En teoría, una red arterial óptima no genera ondas reflejadas. En la práctica, una proporción de las estructuras reales, como las arterias coronarias, pudieran contener hasta un 13% de bifurcaciones no óptimas. En este sentido, la presencia de ondas reflejadas en la señal fotopletismogrífica puede resultar de la naturaleza no óptima de la red arterial. Los cambios de la red arterial con la edad de la persona han tratado de evaluarse cuantitativamente. Se espera que a partir del comportamiento de una población sana, es possible originar ‘indices de “edad cardiovascular”. La discordancia entre la edad cronológica y la edad cardiovascular permitiría evaluar el possible deterioro fisiol’ogico del individuo y su recuperación con acciones restauradoras como el ejercicio y hábitos saludables.
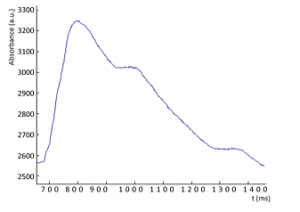
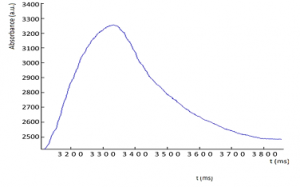
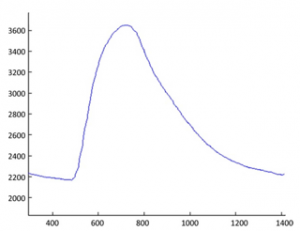
Los cambios en la señal fotopletismográfica con la edad pueden ilustrarse en las siguientes gráficas.
PPG de persona de 10 años
Figura 2. PPG de persona de 10 años.
PPG de persona de 56 años
Figura 3. PPG de persona de 56 años
PPG de persona de 82 años
Figura 4. PPG de persona de 82 años
A partir del año 2000 Hernández Cáceres et al comenzaron a aplicar un método de identificación no lineal para el estudio de la señal PPG.
Sucintamente, en este enfoque se asume a la señal PPG como generada por un sistema dinámico no lineal estocástico
Ese sistema no lineal incluye un importante componente estocástico intrínseco, que constantemente alimenta al sistema.
Ozaki logró generalizar el teorema de Takens para el caso de un sistema estoc’astico, mostrando su correspondencia con un modelo no lineal auto-regresivo:
La originalidad de este enfoque consiste en delimitar la presencia de un “esqueleto” o realización libre de ruido (RLR) determinista y de un componente estocástico de innovación.
La separación del componente determinístico y estocástico de ese sistema es un problema difícil de tratar. En un sistema complejo la naturaleza de la función F es difícil de plantear a priori. Por otra parte, las técnicas generales de aproximación conocidas (aproximación polinomial, núcleos de Volterra, redes neurales, máquinas de soporte vectorial, etc) resultan insuficientes para la obtención de los esqueletos de las funciones.
Entre numerosas variantes evaluadas, el mejor candidato resultó ser el estimador por núcleos de Nadaraya Watson, donde el valor estimado de la función en cada punto del espacio de fase se obtiene como una media ponderada de los valores observados. El peso de cada punto observado ha de depender de la distancia euclídea del punto a evaluar respecto al punto observado.
La aplicación de ese enfoque a señales PPG permitió, entre otros, obtener RLR miméticas de la onda pulsátil.
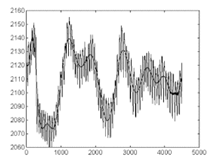
La señal fotopletismográfica registra de manera continua la variación en el volumen de sangre presente en un sitio del cuerpo (por ejemplo la yema del dedo). Por el hecho de que los vasos poseen propiedades elásticas, y el corazón emite ondas de presión durante el ciclo cardíaco, el volumen de sangre ha de variar durante un ciclo cardiaco.
Las complejas propiedades visco-elásticas del flujo sanguíneo, la complejidad geométrica de la red de vasos, y capilares, la regulación autonómica del corazón y los diferentes vasos, además de la regulación intrínseca del ritmo cardíaco, apareen entre los factores que pueden ilustrar la naturaleza compleja de esta señal.
El enfoque basado en la identificación no lineal puede ofrecernos posibilidades muy particulares para la evaluación de esta señal.
Nuestro grupo se planteó la siguiente pregunta: ¿Cuál es el tipo de dinámica que sigue la señal fotopletismográfica?
La aplicación de un enfoque de identificación no lineal permitió separar ambos componentes, obteniéndose lo siguiente:
Componente determinístico
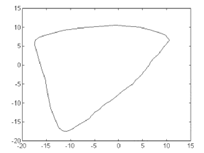
Tras haber analizado más de 600 segmentos de señal fotopletismográfica, obtuvimos que en más del 98% de los casos, las realizaciones libres de ruido se correspondían con un orden óptimo del modelo auto-regresivo igual a 2, lo que sugiere la presencia de atractores de muy baja dimensión. El la mayoría de los casos (72.8%) los atractores eran de tipo ciclo límite, reflejando posiblemente la naturaleza periódica del ciclo cardiaco debidamente acoplado con el sistema vascular. En el 14.4% de los casos las RLR eran caóticas, mientras que en el 12.8% de los casos se trataba de atractores puntuales o casi-puntuales.
El hecho de que una parte importante de los atractores se correspondan con amplitudes mucho menores que las típicas de la onda fotopletismográfica sugiere que el sistema dinámico al que obedece ese sistema debe alimentarse por influencias estocásticas. Ese ruido de innovación sería necesario para mantener al sistema en un régimen de oscilaciones cuasiperiódicas de manera semejante a la forma en que un costal de entrenamiento en boxeo espontáneamente tiende al punto de equilibrio, pero se mantiene oscilando ante los golpes aleatorios que le propina el atleta.
Al menos desde esa perspectiva parece pertinente la interrogante acerca de la naturaleza del componente estocástico de la señal fotopletismográfica.
En 2001 Hernández Cáceres et al aplicaron la metodología de identificación no lineal a señales fotopletismográficas y hubieron de encontrar que el componente no pulsátil se corresponde con un movimiento fractal.
Señal PPG original
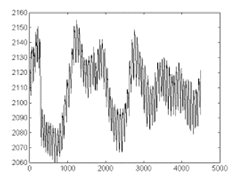
Figura 5. Señal PPG original.
Retrato de fase de la señal que sugiere presencia de caos
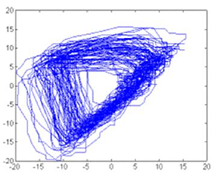
Figura 6. Retrato de fase de la señal que sugiere presencia de caos.
Aproximación de la señal con un polinomio de orden 36
Figura 7. Aproximación de la señal con un polinomio de orden 36.
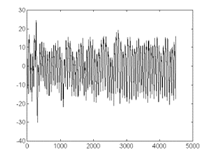
Rresiduo tras la resta del polinomio estimado, quedándose fundamentalmente el componente pulsátil de la señal fotopletismográfica
Figura 8. Rresiduo tras la resta del polinomio estimado, quedándose fundamentalmente el componente pulsátil de la señal fotopletismográfica
(A) Retrato de fase de la Realización libre de ruido obtenida tras aplicar el método de estimación no lineal a la señal en (D) se conserva la presencia de un atractor de tipo ciclo límite.
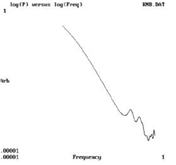
(B) Trazado doblemente logarítmico del espectro del residuo de la identificación no lineal sumado al polinomio estimado en (C), donde se pone de manifiesto la naturaleza fractal del componente no pulsátil de la señal.
Extracción del componente estocástico de una señal fotopletismográfica
Extracción del componente estocástico de una señal fotopletismográfica
Figura 9 . Extracción del componente estocástico de una señal fotopletismográfica.
El efecto de procesar matemáticamente una señal puede conducir a resultados que no se avienen a la realidad. Es a ese tipo de resultados a lo que en ciencia se ha dado en llamar “artefactos”. Un ejemplo de eso lo fueron las numerosas evidencias de la naturaleza caótica del EEG que posteriormente fueran refutadas.
Aún cuando el siguiente resultado no confirma la naturaleza fractal de la señal fotopletismográfica, parece brindar fuertes evidencias a favor.
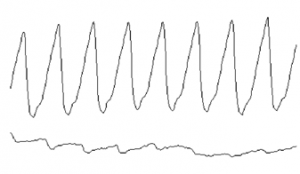
Señal fotopletismográfica tomada en condiciones normales (trazo superior) y ante una presión impuesta de 130 mmHg
Figura 10. Señal fotopletismográfica tomada en condiciones normales (trazo superior) y ante una presión impuesta de 130 mmHg.
Nótese la casi completa abolición de la señal. Ejes Abscisas: Tiempo en centésimas de milisegundos; Ordenadas: amplitud en unidades arbitrarias
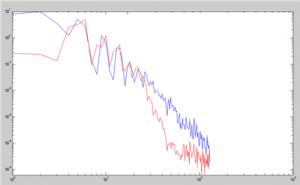
Los espectros doblemente logarítmicos correspondientes a la figura 10, re-escalados a para una misma amplitud
Figura 11 Los espectros doblemente logarítmicos correspondientes a la figura 10, re-escalados a para una misma amplitud.
Nótese que la señal registrada a 130 mmHg se adquiere una apariencia más lineal, como se espera de un proceso fractal.
Como se observa de la figura, la señal registrada a 130 mmHg, donde prácticamente desaparece el componente pulsátil, posee un espectro que se ajusta muy bien a una curva doble logarítmica. En ese sentido el “ruido” extraído matemáticamente (Figura #1) y el “ruido” registrado fisiológicamente presentan ambos propiedades fractales.
Cabañas et al habían reportado que la dimensión fractal del componente estocástico de la señal fotopletismográfica cambia con la gestación. Esto sugiere que la naturaleza fractal del componente estocástico no solamente refleja el ruido de innovación del sistema, sino que también puede cambiar con el estado del individuo, por lo cual pudiera ser de utilidad diagnóstica.
En los últimos años nuestro grupo se ha dedicado a la identificación no lineal de señales emitidas por el sistema cardiovascular. Nuestros resultados han ido obteniéndose a la par que en el plano teórico hayan ido desarrollándose discusiones y han aparecido respuestas a algunas de las interrogantes que nuestros resultados planteaban.
Ha resultado intelectualmente estimulante encontrar que, a diferencia de otros métodos, la identificación no lineal ha sido capaz de encontrar evidencias tanto para el carácter de ciclo límite para las crisis de ausencia como para la caoticidad de otros tipos de epilepsia. Por otra parte, la naturaleza fractal del componente estocástico de la señal fotopletismográfica, que había sido sugerida en base al tratamiento matemático de la señal, ha encontrado apoyo en registros directos donde el componente pulsátil ha sido abolido por la imposición de una presión externa al miembro que se registra.
Por cuanto se trata de un enfoque capaz de brindar respuestas plausibles y de plantear interrogantes interesantes, sugerimos que esta metodología puede ser aplicada para investigaciones fisiológicas a más amplia escala.
Descargar fichero: Utilidad del enfoque de identificación no lineal para el estudio del señales electrofisiológicas complejas
Antecedentes:
Leave a Comment