Se trata de un problema muy difícil de solucionar, pues es una curva con una exponencial elevada al producto de 2 parámetros.
Nuestro enfoque se basa en tratar de linealizar la curva de Richards.
A partir de dos exponenciales se intenta estimar r y tau. Posteriormente se trata de ajustar un un valor de K que, con valores no muy alejados de los estimados iniciales de tau y r, permita ajustar los datos acumulados hasta el momento.
Filed under COVID-19, Modelo matemático by on . Comment. ![]()
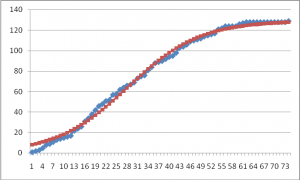
-Tamaño de la epidemia:
K=1097 casos [1063-1131]
-Parámetro r= 0.192 [0,191-0,196] R0= 2,76
-Tiempo hasta el pico 29,6 días [29,4-29,8]
En lenguaje coloquial:
Se espera el pico de la epidemia para el 7 de abril, cuando habrá 550 casos, y para el 6 de mayo debe concluir la epidemia con 1100 casos.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
En nuestra opinión, el exito de Cuba hasta aquí en la lucha contra el COVID19, está basado en ser agresivos con los sujetos que entraban desde fuera de sus fronteras, con todos sus contactos, y con todo sujeto que tuviera síntomas tan solo parecidos. Agresivos se traduce de forma positiva, como un control riguroso dentro del derecho a las libertades personales de los sospechosos, incluído su aislamiento forzoso. Por eso creemos que el número de personas enfermas e incluso fuera de control dentro del país, NO sea muy grande.
Es importante que esto sea público, porque masas de personas siguen emitiendo opiniones que incluso resultan en acusaciones irracionales, basadas según declaran, en lo que ven en casi todos los demás países, donde el enfrentamiento es de forma abierta y donde las cadenas de trasnmisión están abiertas, porque no lograron cortar de raíz las cadenas de trasnmisión como en Cuba. La proyección en una población que no haya logrado lo que Cuba y tenga cantidad de casos confirmados parecida e inició crisis en misma fecha, es probablemente peor. Lo es porque la población suceptible, la que se puede enfermar, en esos casos es la población total. En Cuba, la población susceptible es solo la confinada y eso mejora los números.
El gran temor es una segunda onda o rebrote. Imaginemos que el año que viene se genere un foco de este mismo corona virus en otro país cualquiera. Todo el sujeto que no se infectó en esta etapa, es susceptible, ahora mismo el 89% de la humanidad. Solo hay dos formas de no ser susceptible, enfermarse o resultar inmunisado por una vacuna. Cuando ocurrió la epidemia del Cólera en Haití, nuestra predicción iba viento en popa y de pronto, una locura. No entendíamos nada. Era la segunda onda, casi tan grande como la primera. Ese es el peligro que tienen los países que están logrando aislar a los ciudadanos evitando su contagio.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
El gran temor es una segunda onda o rebrote. Ese es el peligro que tienen los países que están logrando aislar a los ciudadanos evitando su contagio. Las dos esperanzas básicas para las poblaciones susceptibles son: Que el virus mute y se vuelva inocuo. Hasta ahora, desgraciadamente, ocurre lo contrario. En España la mortalidad es el triple de la de China y al día de hoy aumentó la morbilidad en el mundo a 5.5%. La otra: Que se disponga de un candidato vacunal a tiempo para inmunizar esas poblaciones. No se percibe nada al respecto en meses y como dijera el Doctor Duran en conferencia de prensa, se habla del próximo 2021.
Luego, debemos prepararnos los cubanos para un probablemente largo verano en condiciones anormales, con la economía sufriendo. Pero hasta que no dejen de aparecer casos en el entorno, el país sigue en peligro de pandemia. Probablemente erradiquemos la COVID anticipadamente en Cuba respecto al área, pero probablemente eso implique mantenernos cerrados mientras el entorno está en crisis. Cuando decimos cerrados, supondrá una definición de medidas que será país quien determine.
Notar además que los países que más sufren hoy, deberían terminar mejor preparados para un rebrote. Por eso algunas veces se intenta enfrentar las infecciones masivas y no obviarlas, que no es el caso de COVID19 por lo dicho, altísimas tasas de contagios, alto porciento de pacientes que pasan muy rápido a cuidados intensivos, que satura las unidades de cuidados intensivos y la letalidad altísima pese a todos los cuidados y recursos. Lo increíble es que se están reportando casos de rebrotes en pacientes supuestamente curados, esperemos que se deba a considerarlos curados de forma prematura por los servicios sanitarios.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
Las modelaciones epidemias al menos como lo hemos estado haciendo acá, tienen un trasfondo netamente estadístico. Hay variables que se van estimando con la misma progresión de los contagios.
En los tiempos de Carlos Juan Finlay, el paciente se inscribía en la estadística en el momento que un facultativo médico lo diagnosticaba positivo en base a los síntomas y todo el modelo matemático se hizo en base a esos levantamientos que se hacían de esa manera.
Pero las pesquisas confirmatorias en Cuba, probablemente parten de un criterio clínico de selección previo, hecho con calidad y han estado pesquisando a poblaciones con cierto criterio clínico. Por eso la deformidad y la irregularidad en la data de entrada al modelo.
Las primeras oleadas masivas de testeos de los últimos tres días, probablemente se enfocaron primero en los sintomáticos o gente que tenía mucho contacto con casos confirmados. Y eso es lógico, porque la misión de esas pesquisas es justamente continuar afinando el confinamiento y por eso primero van contra los más probables para poder aislaros y
después contra los menos probables, justo para mejorar la probabilidad de aislar temprano. Después se va abriendo el abanico del riesgo biológico a poblaciones con menor probabilidad de contagio y esa podría ser la razón por la que hoy hay un descenso brusco en la cantidad de casos pese a incrementarse los pesquisados, así como la arritmia en los
datos de los últimos 3 o 4 días.
Si fuera esto cierto, la estadística a partir de ahora mezcla dos cosas que no tienen nada que ver, por un lado la maduración de síntomas en los enfermos por el paso de los días y por otro lado el carácter selectivo de la pesquisa. Según los datos públicos hasta hoy, ordenados por
confirmación de la enfermedad y no por aparición de síntomas, el pronóstico cambia de los últimos días a hoy y estamos entonces a dos días del pico, con estimados de número de casos que se van reduciendo.
Puede ser que esto se deba a una mejor precisión por un mayor número de puntos en la curva, o realmente sea una consecuencia de la respuesta del sistema a las medidas que se han tomado. Pero debemos concentrarnos en otra forma de organizar los casos, por fecha de aparición de síntomas,
fecha de ingreso, o algo así. Lo que habíamos reportado hasta aquí, pese a todo parece razonable, tanto que nos quedamos con el reporte de los últimos días que hasta ahí parece más coherente.
A los colegas que critican, recordarles que criticar visceralmente puede convertirse en un arma de doble filo, como dijeron en una película india que vi esta madrugada, la peor, la más letal de las armas, es el tiempo.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
Bueno, después de haber discutido sobre estadísticas, de todas formas ahí va el reporte de hoy 4 de Abril…
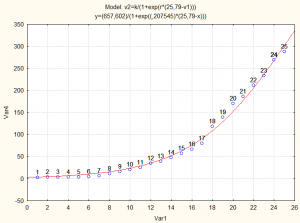
Rango de los parámetros predichos:
Tamaño de la epidemia:
K=630,26 casos [630,26-680,94]
Parámetro r= 0.2075 [0,199-0,217] R0= 2,82
Tiempo hasta el pico 25,8 días [24,6-26,9]
En lenguaje coloquial.
Se espera el pico de la epidemia para el 6 de abril, cuando habrá 315 casos, y para el 4 de mayo debe concluir la epidemia con 630 casos.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
Queridos amigos,
Por solicitud de un amigo cubano en residente en este momento en Ecuador
y basado en la data que nos envía, hemos arriesgado un pronóstico. Aun
cuando la predicción puede ser noble, la calidad de los datos parece
comprometer cualquier intento. A ojos vista, los datos son demasiado
irregulares, cuando se compara el doubling time (que en fin de cuentas
es una característica de la fase exponencial) se ve demasiada
incertidumbre. La comparación con China, o incluso con Cuba donde al
haber menos casos es de esperar mayor fluctuación, nos sugiere que los
datos están raros.
Por ahora, desearle al hermano pueblo ecuatoriano que logre salir de
esta pesadilla lo mejor posible.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
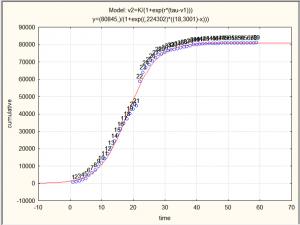
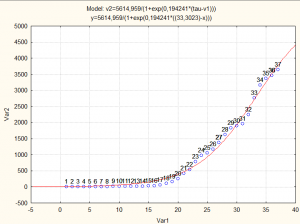
Rango de los parámetros predichos (r=0.99562703)
Tamaño de la epidemia:
K=5615 casos [5470-5760]
Parámetro r= 0,1842 [0,184-0,205] R0= 2,51
Tiempo hasta el pico 33,3 días [33,0-33,6]
En lenguaje coloquial:
Al parecer el pico de la epidemia se alcanzó el día 1 de abril, cuando se predecían según el modelo 2807 casos (y se reportaron 2758), y para el 4 de mayo debe concluir la epidemia con 5615 casos.
Si se observan los datos y la curva ajustada, se nota que hay bastante irregularidad en los datos, pero lo que se brinda aquí es el mejor de los posibles ajustes.
Esto pudiera añadir incertidumbre a cualquier predicción, sobre todo si se toma en cuenta que se trata de funciones altamente no lineales las que se están tratando de ajustar
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()

Comentarios recientes