Tratando de explicar cómo lo hacemos.
Las epidemias se modelan, para que los gobiernos y autoridades sanitarias puedan manejar de la forma más eficiente posible los recursos, con el fin de mitigar los efectos de la epidemia. Por eso se hacen modelaciones, para estimar cuantos enfermos, donde, cuando, cómo y así poder aislar poblaciones, establecer hospitales de campaña, lugar para los fallecidos, movilizar tropas, personal sanitario, medicamentos, optimizar las transportaciones, las comunicaciones y en general, toda la logística de la que se disponga para detener y menguar los efectos negativos de una epidemia. Es para eso que se modela una epidemia.
El modelo SIR fue propuesto en 1927 por Kendrick y McCormick, fue el primero. El más sencillo y por supuesto el de primera elección cuando no se sabe nada y se está en la etapa inicial.
El modelo presupone a los contagios en una epidemia ocurren como una reacción en cadena. Un individuo contagia a cierta cantidad de otros individuos. Cada uno de los individuos de esta cierta cantidad de individuos contagiados por el primero, contagia a su vez a un número igual de terceros individuos. La conducta matemática que refleja este tipo de propagación es la curva exponencial.
A esta población sana de la cual salen los individuos que contagian cada contagiado, se le llama población Susceptible. A los contagiados población Infectada. Y algunos de estos contagiados se recuperan, es decir que se curan, a los que llamamos Recuperados. Por eso el nombre de SIR para el modelo. Modelo de Susceptible – Infectado – Recuperado.
La cierta cantidad de Susceptibles que contagia un Infectado, se llama Número Reproductivo Básico R0 (Erre Cero). Esta variable es muy importante y caracteriza la capacidad contagiosa del virus.
Aclarar que cuando alguien se infecta, ya no es Susceptible. Idénticamente cuando un Infectado se cura ya no es un Infectado. Cuando se sufre una infección por un virus, normalmente quedamos inmunes a ese virus, es decir, ya no nos afectará más. Por esa razón, un Recuperado tampoco puede ser un Susceptible. El modelo por tanto opera con poblaciones que se excluyen una a la otra, un individuo no puede estar incluido en dos de estas categorías al mismo tiempo. Un individuo está Susceptible o Infectado o Recuperado, pero nunca en dos categorías al mismo tiempo.
A un Infectado que no se ha recuperado se le llama también Caso Activo. A los Infectados todos se les llama Caso Confirmado. Un Infectado mientras no se cure o Recupere, es un Caso Activo. Cuando se cura, deja de ser Caso Activo y pasa a Recuperado.
El manejo de los fallecidos tiene variantes, para Kendrick y McCormick lo importante era saber los Activos, que son los que ocupan a los tomadores de decisiones. Ya se recupere un Caso activo o fallezca, para SIR se puede manejar igual como recuperado porque ya no está activo. También se pueden hacer dos grupos que sustituyan a los Recuperados y contabilicen a los verdaderamente Recuperados por un lado y a los Fallecidos por otro, pero en las ecuaciones matemáticas del modelo SIR clásico, todos los Infectados que no sean Activos, se llaman Recuperados. Es decir, que el número que se introduce en las ecuaciones en el parámetro de Recuperados es la suma de los Recuperados y Fallecidos de la realidad.
Una cosa es comunicar al público la situación epidemiológica y otra es la modelación matemática y sus objetivos.
Dada una población que no crece durante el periodo de evolución de la epidemia, como puede ser la de un país confinado a sus fronteras, cuando los Infectados crecen, los Susceptibles disminuyen. Llega el momento en que un Infectado no encuentra a su alcance suficientes Susceptibles para poder cumplir su tasa de contagio R0. Ese es el pico de la epidemia, cuando al cabo de determinado tiempo de evolución de la epidemia, a un ritmo de contagio marcado por R0, la cantidad remanente de Susceptibles, ya NO es suficiente para que la creciente población de Infectados, consiga contagiar todos los R0 Susceptibles que cada Infectado podría como máximo contagiar.
Luego, en ausencia de medidas tomadas por las poblaciones humanas que cambien la dinámica de los contagios, R0 es una constante hasta el momento en que por extinción de los Susceptibles, ya no se pueda reproducir la infección en su forma natural.
Aquí, muchas discusiones.
Las medidas implementadas por las autoridades sanitarias, podrían incidir en R0. Al tomarse medidas efectivas que frenan el contagio, un Infectado ya no consigue llegar a la misma cantidad de Susceptibles R0 que en ausencia de estas medidas, por lo que R0 disminuye aunque exista suficiente población de Susceptibles. Ejemplo, si erradicas o disminuyes la población del mosquito que transmite la fiebre amarilla. Esa medida hace que un Infectado tenga menos posibilidades de ser picado por un mosquito portador y de que se transmita la fiebre amarilla. En el caso de COVID19, las medidas de distanciamiento social son un muy buen ejemplo.
En 1927 y antes, poco podía hacer el Estado y sus autoridades sanitarias y R0 era casi invariable hasta que se alcanzaba el pico en las condiciones naturales de expansión de la enfermedad. Por eso Kendrick y McCormick modelaron R0 de suponiéndola una constante durante el tiempo en que no se alcanzara el pico. No solo R0, sino que muchos otros parámetros de su modelo matemático se suponen constantes durante la etapa de subida de la exponencial.
Entonces, una de las razones o la más importante razón por la cual los modelos divergen de la realidad con tanta frecuencia, es porque en nuestra época, el estado tiene una fuerza grande para manejar el curso natural de una epidemia y lo hace además cuando le parece oportuno, valorando incluso variables que no son epidémicas, como la economía. Cada medida que toma un estado o autoridad sanitaria, puede modificar la capacidad del virus de trasmitirse, es decir, modifica la R0, cosa con la que no contaban Kendrick y McCormick.
Entonces, la disminución de R0 hoy, NO es necesariamente índice de que se haya alcanzado el pico. La disminución de R0 es evidencia de superado el pico, en una epidemia en que la acción de las medidas tomadas por las autoridades sanitarias es nula o muy baja o porque hace ya mucho tiempo que estas medidas fueron tomadas y se cuenta con una etapa en que R0 se ha estabilizado en cierto valor, que caracteriza la expansión del virus en las condiciones que le ha impuesto las medidas de las autoridades sanitarias.
Las medidas tomadas por las autoridades sanitarias si son exitosas, tienden a aplanar y alargar la forma gráfica de las curvas de Infectados, Casos Activos y bueno, Recuperados. Las autoridades si toman
medidas efectivas no solo epidémicas sino también terapéuticas, pueden cambiar todo el dibujo de las diferentes variables que describen una epidemia a través de un modelo matemático.
Todo esto se ha visto en Cuba durante la evolución de la epidemia. La Universidad de OXFORD elaboró un índice para evaluar la severidad o rigor del estado en su esfuerzo para menguar los efectos de una epidemia. Este índice se denomina Índice de Rigor, y se incrementa en la medida en que el estado va implementando el grupo de medidas que este índice pre supone se pueden tomar por parte del estado. La aplicación de cada medida en cada momento, dibuja una curva a saltos llamada curva de Rigor.
La curva de índice de rigor no dice nada bueno o malo. Solo informa del rigor de las medidas adoptadas por cada país en cada momento. Su relación con el comportamiento de los casos y todas sus salidas son las que informan cuan efectivas fueron las medidas y también, cuanto colaboro la población local al comportamiento de la crisis.
Solo mirar la curva de Rigor en Cuba y el comportamiento de la epidemia, demuestra de la forma más inobjetable y pragmática de que se dispone hoy, que el estado Cubano actuó correctamente, en base a los recursos con los que contaba.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
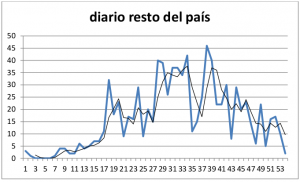
1: Casos diarios Resto del país
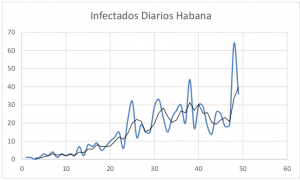
2: Casos diarios La Habana
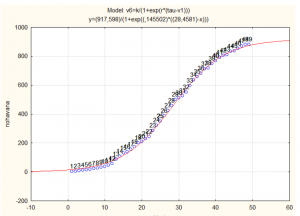
3: Predicciones del modelo de Richards Resto del país
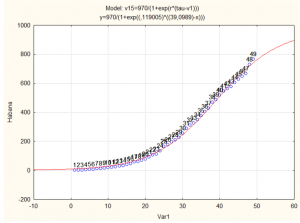
4: Predicciones del modelo de Richards La Habana
Discusión
Sin entrar en demasiados detalles, el comportamiento de los casos diarios en el resto del país muestran una forma de
campana cuyo pico ocurrió hace varios días: de los 46 diarios que se veían el día 39, ayer bajó a dos casos.
En La Habana no se nota una evidencia clara y no se ve esa forma de campana.
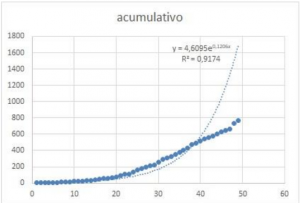
La curva de datos acumulativos en el resto del país los últimos días ha bajado considerablemente la pendiente, prácticamente está casi en la asíntota de la función
de Richards
Esa caída en la pendiente prácticamente no se ve en La Habana La Habana
El modelo de Richards brinda una diferencia en el punto de viraje o momento de máxima incidencia, de 11 días (39 vs 28 días, eso es algo muy notable!!!)
Sin entrar en detalles matemáticos, pues a estas alturas no puedo demostrarlo, tal parece como si hubiera un repunte en La Habana, el evento en el Centro de Atención a
Deambulantes en el Cotorro fue algo local, pero ayer casi no se reportaron casos en el cotorro (3) y de nuevo La Habana reportó 36 casos, el tercer valor más alto de la epidemia en La Habana.
Llama la atención que de los 36 casos reportados ayer en la Habana hay 10 menores de 13 años, eso denota, cuando menos, indisciplina y descuido.
Próximamente intentaremos detallar provincias o regiones (p-ej Oriente, Camagüey, Las Villas, Mayabeque-Matanzas, Vuelta abajo) y trataremos de seguir los municipios
habaneros.
Conclusiones.
La gran batalla es en La Habana, debemos ver cada provincia por separado. Los dos últimos días sugieren un repunte. Los próximos siete días en La Habana serán decisivos.
La única esperanza es que la misma dirección del país que logró tan buenos resultados en el resto del país es la que está controlando la situación en La Habana, y seguramente se tomarán las medidas pertinentes para atajar esta situación.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
Las medidas tomadas en Cuba permiten modelar la evolución de la COVID19, separando la modelación por provincias ya que estas están aisladas. Esto es aconsejable por la notoria diferencia que comienza a marcar La Habana sobre el resto de los territorios.
En las gráficas de acumulados no deben esperarse picos, es absurdo, pero el descenso en el progreso de la epidemia se evidencia por el cambio de conducta en la curva que abandona su crecida exponencial y se aplana.
La Habana, Mayo 2 de 2020. La curva es tendiente a un crecimiento exponencial sin evidencia de
cambio de conducta.
Resto de las provincias cubanas Mayo 2 de 2020. En todas con mayor o menor grado se evidencia
aplanamiento de la curva.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
BOLIVIA vs CUBA:
No hay forma de comparar sin pecar de un poco injustos. Se propone seleccionar países que tengan similitud en: Tamaño de población, Densidad de población, Área geográfica y coincidencia en Días de iniciada el contagio, por ese orden.
Criterios de Similitud entre países: ÁREA GEOGRÁFICA, CANTIDAD DE POBLACIÓN. DÍA CERO.
EVALUACIÓN DE CUBA: País: BIEN, Población: IGUAL, Hospitalización: MEJOR.
En la etapa hasta el día 42 de iniciado el contagio, Cuba tiene más contagios, pese a la misma cantidad de habitantes.
Ambos países en una curva de ascenso suave alejadas de exponenciales de trepadas intensas.
El índice de rigor muestra que Bolivia Comenzó antes con la toma de medidas, pero Cuba que aplicó algo más tarde las medidas adoptadas por Bolivia, las superó un tiempo después.
La curva de rigor no dice nada bueno o malo. Solo informa del rigor de las medidas adoptadas por cada país en cada momento. Su relación con el comportamiento de los casos y todas sus salidas son las que informan cuan efectivas fueron las medidas y también, cuanto colaboro la población local al comportamiento de la crisis.
Los casos activos también son mayores en Cuba.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()
Diario El PAÍS (Madrid). Versión Web. https://elpais.com/?/?/13/actualidad/1586788600_290634.html?
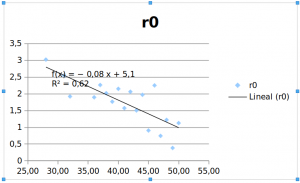
Publica dos datos que refuerzan nuestros estimados. R0 para el número de casos en Cuba es igual a 1 en esos momentos. Esto se aviene con la idea de que el pico de la epidemia se alcanzó hace varios días.
Nuestros estimados de R0 por el modelo de Richards parten de asumir que el tiempo de generación es 5 días, hoy se ha comprobado que es 4-7 días.
Más abajo se relaciona la evolución de nuestros estimados emitidos día a día.
Filed under COVID-19, Epidemia, Modelo matemático by on . Comment. ![]()





Comentarios recientes